Force
$\displaystyle \small \bullet$ Force is an external source/action which changes or tends to change the state of an object.
$\displaystyle \small \bullet$ It is a vector quantity i.e. it contains magnitude, direction and point of action.
$\displaystyle \small \bullet$ It is the product of mass of the object and the acceleration
$\displaystyle \small F=m\times a$
$\displaystyle \small \bullet$ Units of Force
$\displaystyle \small \circ$ MKS(SI): Newton (N), $\displaystyle \small kg-m/sec^{2}$
$\displaystyle \small \circ$ CGS: Dyne (D), $\displaystyle \small gm-cm/sec^{2}$
$\displaystyle \small \circ$ FPS: Poundal, $\displaystyle \small lb-ft/sec^{2}$
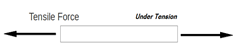
Types of Forces
1. Tensile force
When two equal and opposite forces having same line of action, act on an object, they tend to increase the length of the object.
The object is said to be under tension.
2. Compressive force
When two equal and opposite forces having same line of action, act on an object, they tend to decrease the length of the object.
The object is said to be under compression.
3. Shear force
When two equal and opposite forces having different line of action, act on an object, one section of object tends to slide over another section which results in shearing.
The object is said to be under shear.
Effects of Force
Tensile effect/Tension
Compressive effect/Compression
Shear effect/Shearing
Twisting effect
Bending effect
Breaking effect
Change in condition/state
Change in speed
Change in direction
Change in dimension
Resultant Force
Force acting in a straight line: direction of resultant force is same as greater force.
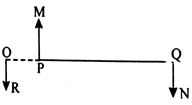
Parallel forces
Like Parallel forces
$\displaystyle \small R=P+Q$
$\displaystyle \small M\times PO=N\times OQ$
Unlike Parallel forces
$\displaystyle \small R=P+Q$
$\displaystyle \small M\times PO=N\times OQ$
Mutually intersecting forces
$\displaystyle \small \bullet$ When two or more forces act upon single point such that they form an angle with respect to each other, then their resultant force acts on the same point.
$\displaystyle \small \bullet$ This is calculated by Parallelogram Law of forces and Triangle Law of forces.
Composition of Forces
Parallelogram Law of Forces
$\displaystyle \small R=\sqrt{P^{2}+Q^{2}+2PQ\cos \theta }$
$\displaystyle \small \tan \alpha =\frac{Q\sin \theta }{P+Q\cos \theta }$
Triangle Law of Forces
$\displaystyle \small \frac{P}{AB}=\frac{Q}{BC}=\frac{R}{AC}$
Lami’s Theorem
$\displaystyle \small \frac{P}{\sin \theta }=\frac{Q}{\sin \alpha }=\frac{R}{\sin \beta }$
Jib Crane
Resolution of Forces
$\displaystyle \small P=\frac{R\sin \beta }{\sin (\alpha +\beta )}$
$\displaystyle \small Q=\frac{R\sin \alpha }{\sin (\alpha +\beta )}$
Condition for Equilibrium of Forces Acting on a Body
$\displaystyle \small \bullet$ Sum of components of forces acting in the horizontal direction is equal to zero.
$\displaystyle \small \sum H=0$
$\displaystyle \small \bullet$ Sum of components of forces acting in the vertical direction is equal to zero.
$\displaystyle \small \sum V=0$
$\displaystyle \small \bullet$ Sum of moment acting at a point is zero.
$\displaystyle \small \sum M=0$
$\displaystyle \small \bullet$ Force is an external source/action which changes or tends to change the state of an object.
$\displaystyle \small \bullet$ It is a vector quantity i.e. it contains magnitude, direction and point of action.
$\displaystyle \small \bullet$ It is the product of mass of the object and the acceleration
$\displaystyle \small F=m\times a$
$\displaystyle \small \bullet$ Units of Force
$\displaystyle \small \circ$ MKS(SI): Newton (N), $\displaystyle \small kg-m/sec^{2}$
$\displaystyle \small \circ$ CGS: Dyne (D), $\displaystyle \small gm-cm/sec^{2}$
$\displaystyle \small \circ$ FPS: Poundal, $\displaystyle \small lb-ft/sec^{2}$
Types of Forces
When two equal and opposite forces having same line of action, act on an object, they tend to increase the length of the object.
The object is said to be under tension.
When two equal and opposite forces having same line of action, act on an object, they tend to decrease the length of the object.
The object is said to be under compression.
When two equal and opposite forces having different line of action, act on an object, one section of object tends to slide over another section which results in shearing.
The object is said to be under shear.
Effects of Force
Tensile effect/Tension
Compressive effect/Compression
Shear effect/Shearing
Twisting effect
Bending effect
Breaking effect
Change in condition/state
Change in speed
Change in direction
Change in dimension
Resultant Force
Force acting in a straight line: direction of resultant force is same as greater force.
Like Parallel forces
$\displaystyle \small M\times PO=N\times OQ$
Unlike Parallel forces
$\displaystyle \small M\times PO=N\times OQ$
Mutually intersecting forces
$\displaystyle \small \bullet$ When two or more forces act upon single point such that they form an angle with respect to each other, then their resultant force acts on the same point.
$\displaystyle \small \bullet$ This is calculated by Parallelogram Law of forces and Triangle Law of forces.
Composition of Forces
$\displaystyle \small \tan \alpha =\frac{Q\sin \theta }{P+Q\cos \theta }$
Triangle Law of Forces
Lami’s Theorem
Jib Crane
Resolution of Forces
$\displaystyle \small Q=\frac{R\sin \alpha }{\sin (\alpha +\beta )}$
Condition for Equilibrium of Forces Acting on a Body
$\displaystyle \small \bullet$ Sum of components of forces acting in the horizontal direction is equal to zero.
$\displaystyle \small \sum H=0$
$\displaystyle \small \bullet$ Sum of components of forces acting in the vertical direction is equal to zero.
$\displaystyle \small \sum V=0$
$\displaystyle \small \bullet$ Sum of moment acting at a point is zero.
$\displaystyle \small \sum M=0$
0 Comments