To solve a system of linear inequalities in two variables graphically, proceed as follows:
Step 1: Draw the graph of all the given linear inequalities.
Step 2: Find the common part of the co-ordinate plane, which satisfies all the given linear inequalities.
Step 3: This common part of the plane is the required solution of the given inequalities.
step 4: If there is no common region, then the solution set of the system of inequalities is empty set.
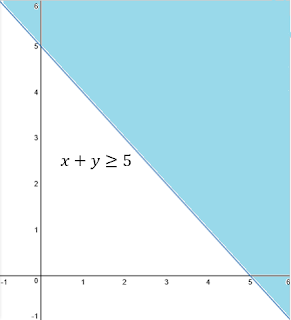
Example 1: $x+y\geq 5$, $x-y\leq 3$
Consider, $x+y=5$
Put x=0, y=5
Put y=0, x=5
Consider origin (0,0)
$0\geq 5$ which is not true
The portion which does not contain (0,0), represents solution set of $x+y\geq 5$
Consider, $x-y=3$
Put x=0, y=-3
Put y=0, x=3
Consider origin (0,0)
$0\leq 3$ which is true
The portion which contain (0,0), represents solution set of $x-y\leq 3$
Thus, the green shaded region, common to the above two shaded regions, is the required solution region of the given system of inequalities.
.
Step 1: Draw the graph of all the given linear inequalities.
Step 2: Find the common part of the co-ordinate plane, which satisfies all the given linear inequalities.
Step 3: This common part of the plane is the required solution of the given inequalities.
step 4: If there is no common region, then the solution set of the system of inequalities is empty set.
Example 1: $x+y\geq 5$, $x-y\leq 3$
Consider, $x+y=5$
Put x=0, y=5
Put y=0, x=5
Consider origin (0,0)
$0\geq 5$ which is not true
The portion which does not contain (0,0), represents solution set of $x+y\geq 5$
Consider, $x-y=3$
Put x=0, y=-3
Put y=0, x=3
Consider origin (0,0)
$0\leq 3$ which is true
The portion which contain (0,0), represents solution set of $x-y\leq 3$
Thus, the green shaded region, common to the above two shaded regions, is the required solution region of the given system of inequalities.
.





0 Comments