Straight Lines

Important formulas of Straight Lines
1. Distance between the points $\displaystyle P(x_{1},y_{1})$ and $\displaystyle Q(x_{2},y_{2})$ is
$\displaystyle PQ=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$

2. The coordinates of a point dividing the line segment joining the points $\displaystyle (x_{1},y_{1})$ and $\displaystyle (x_{2},y_{2})$ internally, in the ratio m:n are $\displaystyle \left ( \frac{mx_{2}+nx_{1}}{m+n}, \frac{my_{2}+ny_{1}}{m+n} \right )$

3. In particular if m=n, the coordinates of the mid-point of the line segment joining the points $\displaystyle (x_{1},y_{1})$ and $\displaystyle (x_{2},y_{2})$ are $\displaystyle \left ( \frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2} \right )$

4. Area of the trianle whose vertices are $\displaystyle (x_{1},y_{1})$, $\displaystyle (x_{2},y_{2})$ and $\displaystyle (x_{3},y_{3})$ is $\displaystyle \frac{1}{2}\mid x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})\mid$

SLOPE OF A LINE
A line in a coordinate plane forms two angles with the x-axis, which are supplementary.
Thr angle $\displaystyle \theta$ made by the line l with positive direction of x-axis and measured anti clockwise is called the inclination of the line. $\displaystyle 0\leqslant \theta \leq 180^{0}$.
The lines parallel to x-axis or coinciding with x-axis have inclination of $\displaystyle 0^{0}$.
The lines parallel to y-axis or coinciding with y-axis have inclination of $\displaystyle 90^{0}$.

SLOPE OF A LINE WHEN COORDINATES OF ANY TWO POINTS ON THE LINE ARE GIVEN
Let $\displaystyle P(x_{1},y_{1})$ and $\displaystyle Q(x_{2},y_{2})$ be two points on non-vertical line l whose inclination is $\displaystyle \theta$.
($\displaystyle x_{1}\neq x_{2}$, otherwise the line will become perpendicular to x-axis and its slope will not be defined).
The inclination of the line l may be acute or obtuse.
Draw perpendicular QR to x-axis and PM perpendicular to RQ.

Case I: When angle $\displaystyle \theta$ is acute

$\displaystyle \angle MPQ=\theta$ ...(i)
slope of line,$\displaystyle l=m=tan \theta$
In $\displaystyle \Delta MPQ$, $\displaystyle tan \theta=\frac{MQ}{MP}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ ...(ii)
From (i) and (ii),
$\displaystyle m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

Case II: When angle $\displaystyle \theta$ is obtuse

$\displaystyle \angle MPQ=180^{0}-\theta$
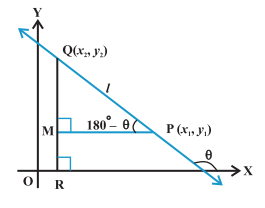
$\displaystyle \theta=180^{0}-\angle MPQ$
slope of line l,
$\displaystyle m=tan \theta$
$\displaystyle =tan (180^{0}-\angle MPQ)=-tan \angle MPQ$
$\displaystyle =\frac{MQ}{MP}$
$\displaystyle =\frac{MQ}{MP}=-\frac{y_{2}-y_{1}}{x_{1}-x_{2}}$
$\displaystyle =\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

In both cases the slope m of the line through the points $\displaystyle (x_{1},y_{1})$ and $\displaystyle (x_{2},y_{2})$ is given by $\displaystyle m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

CONDITIONS FOR PARALLELISM AND PERPENDICULARITY OF LINES IN TERMS OF THEIR SLOPES
In a coordinate plane, suppose that non-verticala line $\displaystyle l_{1}$ and $\displaystyle l_{2}$ have slopes $\displaystyle m_{1}$ and $\displaystyle m_{2}$ respectively.
Let their inclinations be $\displaystyle \alpha$ and $\displaystyle \beta$ respectively.
If the line $\displaystyle l_{1}$ is parallel to $\displaystyle l_{2}$,

then their inclinations are equal. i.e. $\displaystyle \alpha=\beta$
Hence, $\displaystyle tan\alpha=tan\beta$
Therefore, $\displaystyle m_{1}=m_{2}$, i.e. their slopes are equal.
Conversely, if the slope of two lines $\displaystyle l_{1}$ and $\displaystyle l_{2}$ is same, $\displaystyle m_{1}=m_{2}$
then $\displaystyle tan\alpha=tan\beta$
By the property of tangent function, $\displaystyle \alpha=\beta$.
Therefore the lines are parallel.
Hence, two non-verticala lines $\displaystyle l_{1}$ and $\displaystyle l_{2}$ are parallel if and only if their slopes are equal.

If the line $\displaystyle l_{1}$ and $\displaystyle l_{2}$ are parallel,

then $\displaystyle \beta=\alpha+90^{0}$
Therefore, $\displaystyle \beta=tan(\alpha+90^{0})$
$\displaystyle =-cot\alpha =-\frac{1}{tan\alpha }$
i.e. $\displaystyle m_{2}=-\frac{1}{m_{1}}$ or $\displaystyle m_{1}m_{2}=-1$
Conversely, if $\displaystyle m_{1}m_{2}=-1$, $\displaystyle tan\alpha tan\beta=-1$
Then, $\displaystyle tan\alpha=-cot\beta$
$\displaystyle =tan(\beta +90^{0})$  or $\displaystyle =tan(\beta -90^{0})$
Therefore, $\displaystyle \alpha$ and $\displaystyle \beta$ differ by $\displaystyle 90^{0}$.
Thus, lines $\displaystyle l_{1}$ and $\displaystyle l_{2}$ are perpendicular to each other.

ANGLE BETWEEN TWO LINES
Let $\displaystyle l_{1}$ and $\displaystyle l_{2}$ be two non-vertical lines with slopes $\displaystyle m_{1}$ and $\displaystyle m_{2}$ respectively.
If $\displaystyle \alpha_{1}$ and $\displaystyle \alpha_{2}$ are the inclinations of lines $\displaystyle L_{1}$ and $\displaystyle L_{2}$ respectively.
Then, $\displaystyle m_{1}=tan\alpha_{1}$ and $\displaystyle m_{2}=tan\alpha_{2}$
When two lines intersect each other, they make two pairs of vertically opposite angles such that sum of any two adjacent angles is $\displaystyle 180^{0}$.
Let $\displaystyle \theta$ and $\displaystyle \phi$ be the adjacent angles between the lines $\displaystyle L_{1}$ and $\displaystyle L_{2}$

Then $\displaystyle \theta =\alpha_{2}-\alpha_{1}$ and $\displaystyle \alpha_{1},\alpha_{2}\neq 90^{0}$
Therefore, $\displaystyle tan\theta =tan(\alpha _{2}-\alpha _{1})$
$\displaystyle =\frac{tan\alpha _{2}-tan\alpha _{1}}{1+tan\alpha _{1}tan\alpha _{2}}$
$\displaystyle =\frac{m_{2}-m_{1}}{1+m_{1}m_{2}}$
and $\displaystyle \phi =180^{0}-\theta$
so $\displaystyle tan \phi =tan \left (180^{0}-\theta \right )=-tan \theta =-\frac{m_{2}-m_{1}}{1+m_{1}m_{2}}$
Case I: If $\displaystyle \frac{m_{2}-m_{1}}{1+m_{1}m_{2}}$ is positive, then $\displaystyle tan \theta$  will be positive and $\displaystyle tan \phi$ will be negative, which means $\displaystyle \theta$  will be acute and $\displaystyle \phi$ will be obtuse.
Case II: If $\displaystyle \frac{m_{2}-m_{1}}{1+m_{1}m_{2}}$ is negative, then $\displaystyle tan \theta$  will be negative and $\displaystyle tan \phi$ will be positive, which means $\displaystyle \theta$  will be obtuse and $\displaystyle \phi$ will be acute.

∴ The acute angle between lines $\displaystyle L_{1}$ and $\displaystyle L_{2}$  with slopes $\displaystyle m_{1}$ $\displaystyle m_{2}$  is given by
$\displaystyle tan \theta =\left | \frac{m_{2}-m_{1}}{1+m_{1}m_{2}} \right |$
The obtuse angle can be found by using $\displaystyle \phi =180^{0}-\theta$

COLLINEARITY OF THREE POINTS
If two lines having the same slope pass through a common point, then two lines will coincide.

If A,B,C are three points in the XY-plane, then they will lie on a line.
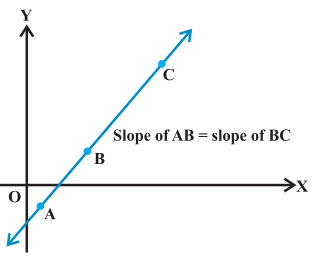
Three points are collinear if and only if slope of AB=slope of BC